感知机

感知机（perceptron）

感知机

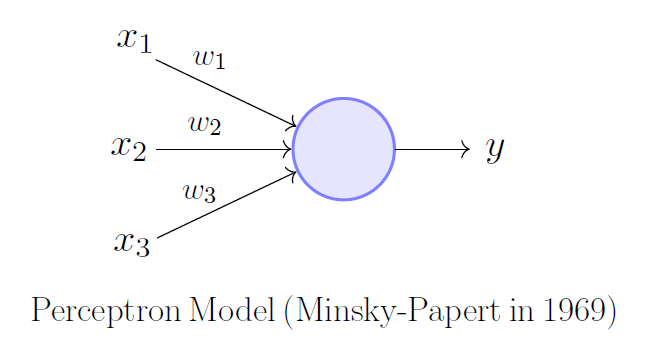
上图是一个感知机，由以下几部分组成：

$x_1,x_2,x_3$ 输入信号
$w_1,w_2,w_3$ 权重（weight）
$y$ 输出
$\theta$ 阈值（图中未标出）

感知机的输出与输入满足：

\[y=\begin{cases} 0 & (w_1x_1+w_2x_2\leq \theta)\\ 1 & (w_1x_1+w_2+x_2>\theta) \end{cases}\]

感知机可以用来实现一些简单的逻辑。比如下面代码实现的是与门。

def AND(x1, x2):
  w1, w2, theta = 0.5, 0.5, 0.7
  tmp = x1*w1 + x2*w2
  if tmp <= theta:
    return 0
  elif tmp > theta:
    return 1

print(
    AND(0,0),
    AND(0,1),
    AND(1,0),
    AND(1,1)
)

OUTPUT:
    0 0 0 1

为了使感知机更具有普适性，我们将表达式修改为：

\[y=\begin{cases} 0 & (b+w_1x_1+w_2x_2\leq 0)\\ 1 & (b+w_1x_1+w_2+x_2>0) \end{cases}\]

通过增加一个 $b$ 偏置（bias），就可以统一用 0 作为阈值。

利用修改后的表达式，我们可以利用 numpy 写出与门、或门、与非门。

import numpy as np

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

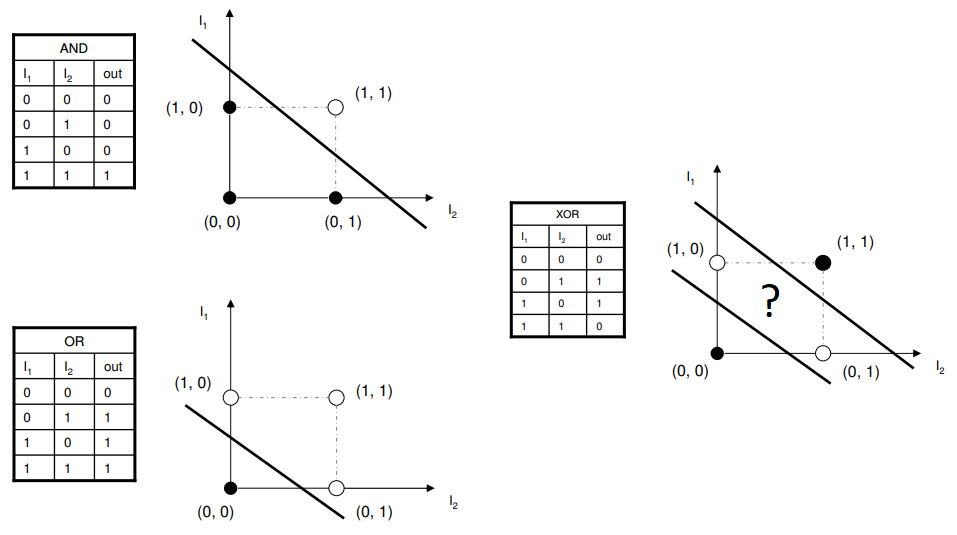
单个感知机无法实现异或门。这是因为感知机本质上是利用一条直线将 $x_1-x_2$ 组成的平面划分成两部分。而要实现异或门，则需要多条直线来划分。

感知机局限

XOR

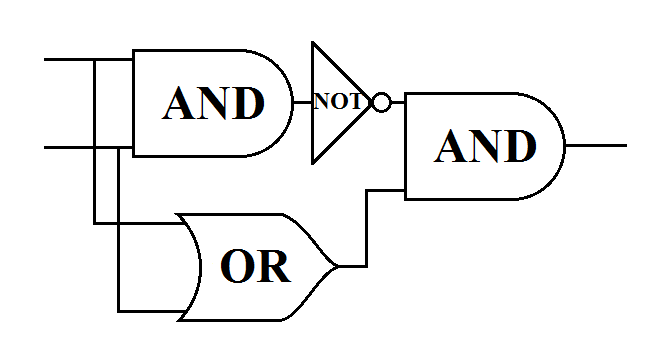
def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

print(
    XOR(0,0),
    XOR(0,1),
    XOR(1,0),
    XOR(1,1)
)

OUTPUT:
    0 1 1 0

于是，通过多重感知机，我们可以实现所有的逻辑功能，从而可以实现计算机。因此感知机是深度学习里最基础的组成部分。

上篇Matplotlib

下篇神经网络